Lenguajes Regulares Unidad 2

Lenguaje regular. En Lingüística, Matemáticas e Informática y en la jerarquía de Chomsky se refiere a los lenguajes de tipo 3, aquellos que pueden representarse mediante gramáticas regulares, autómatas finitos o expresiones regulares.

Son los lenguajes formales más simples, con los mecanismos de representación y reconocimiento más estudiados. Su aplicación práctica en la teoría y construcción de intérpretes y compiladores de lenguajes de programación o de especificación o formato de información, especialmente como microcomponentes del analizador lexicográfico que detecta los tókenes como constantes numéricas, cadenas de texto, operadores, palabras reservadas (keywords), separadores, etc. Pero también se puede apreciar su uso en máquinas expendedoras, teléfonos públicos, calculadoras y otros artefactos electromecánicos.

Definiciones.

Se dice que un lenguaje es regular si y sólo si se cumple cualquiera de las siguientes proposiciones:

• Tiene al menos una gramática regular G que lo produce.
• Puede ser reconocido por un autómata finito A.
• Existe una expresión regular Er que representa a todas las cadenas de L.

Dentro de la Jerarquía de Chomsky se refiere a los lenguajes de tipo 3, el subconjunto de lenguajes formales mas restringido dentro de la jerarquía, como se ve en la imagen.

También puede realizarse una definición recursiva-constructiva de los lenguajes regulares mediante el álgebra de lenguajes formales.

Un lenguaje regular sobre un alfabeto T ó LR(T) es:

1. El lenguaje vacío {}.
2. El lenguaje conformado por la cadena vacía 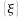 o lenguaje trivial.
3. Un lenguaje {x} conformado por un único símbolo x de T.
4. Si A y B son lenguajes regulares sobre T, entonces AB (Concatenación de lenguajes),  (Unión de lenguajes), A* (Clausura de lenguaje o Estrella de Kleene) son también lenguajes regulares sobre T.
5. Cualquier otro lenguaje que pueda obtenerse a partir de 1 a 4.

6. Ejemplo 1.

   Demuestre que el lenguaje conformado por los nombres de variables de PROLOG es un lenguaje regular.
   Primero debe recordarse que un nombre de variable PROLOG viene dada por la forma:
   Cualquier palabra que comience con una letra mayúscula seguida o no de combinaciones de letras, cifras o subrayados o que comience con al menos un subrayado seguido o no de cualquier secuencia de alfanuméricos o subrayados.
   Cada de las siguientes construcciones son equivalentes en virtud de la definición dada antes:
   • La expresión regular (A|B|...|Z)|_(A|B|...|Z|a|b|...|z|_)*.
   • El siguiente autómata finito representado como diagrama de estados permite el reconocimiento de variables de PROLOG.
   • Una gramática con producciones de la forma:
     • .
     • .