Propiedades de lenguajes regulares
Sean 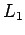 y
y 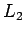 dos lenguajes regulares.
dos lenguajes regulares.
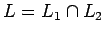 .
.
La idea principal es, simular en paralelo en un solo autómata (digamos autómata de producto) las transiciones de los dos autómatas (por ejemplo finitos deterministas y completas) para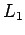 y
y 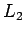 .
.
Entonces sean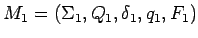 y
y 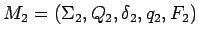 los dos AFDs completos que aceptan
los dos AFDs completos que aceptan 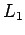 y
y 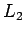 , es decir,
, es decir, 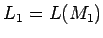 y
y 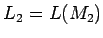 .
.
Construimos el AFD completo que acepta
que acepta 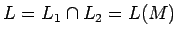 como
como
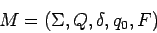
donde
- Unión:
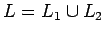 es regular, porque podemos construir una expresión regular para
es regular, porque podemos construir una expresión regular para  , teniendo las expresiones regulares para
, teniendo las expresiones regulares para 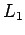 y
y 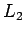 , más preciso: con
, más preciso: con 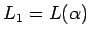 y
y 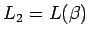 tenemos
tenemos 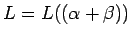
- Concatención:
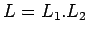 es regular, porque podemos construir una expresión regular para
es regular, porque podemos construir una expresión regular para  , teniendo las expresiones regulares para
, teniendo las expresiones regulares para 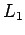 y
y 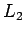 , más preciso: con
, más preciso: con 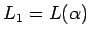 y
y 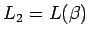 tenemos
tenemos 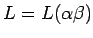
- Clausura:
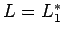 es regular, porque podemos construir una expresión regular para
es regular, porque podemos construir una expresión regular para  , teniendo la expresión regular para
, teniendo la expresión regular para 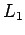 , más preciso: con
, más preciso: con 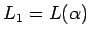 tenemos
tenemos 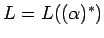
- Complemento:
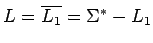 es regular, porque podemos construir, dado un AFD completo
es regular, porque podemos construir, dado un AFD completo 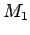 que acepta
que acepta 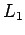 , un AFD
, un AFD  que acepta
que acepta  simplemente `invertiendo' sus estados finales, es decir, los estados no finales de
simplemente `invertiendo' sus estados finales, es decir, los estados no finales de 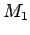 serán los estados finales de
serán los estados finales de  y los finales se convierten en los no finales, entonces, si
y los finales se convierten en los no finales, entonces, si 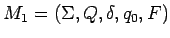 construimos
construimos 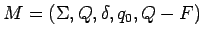 .
.- Intersección:
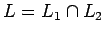 es regular, porque con las reglas de DeMorgan obtenemos
es regular, porque con las reglas de DeMorgan obtenemos 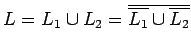 . Complemento y unión producen lenguajes regulares, como visto antes. Dicha construcción es bastante laborosa, abajo vemos una construcción directa y simple.
. Complemento y unión producen lenguajes regulares, como visto antes. Dicha construcción es bastante laborosa, abajo vemos una construcción directa y simple.- Diferencia:
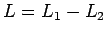 es regular, porque se puede expresar la diferencia como
es regular, porque se puede expresar la diferencia como 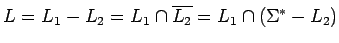 y las operaciones usadas mantienen la regularidad.
y las operaciones usadas mantienen la regularidad.
La idea principal es, simular en paralelo en un solo autómata (digamos autómata de producto) las transiciones de los dos autómatas (por ejemplo finitos deterministas y completas) para
Entonces sean
Construimos el AFD completo
donde
- asumimos que
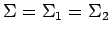 , es decir, usamos solamente los símbolos comunes. Es fácil eliminar en
, es decir, usamos solamente los símbolos comunes. Es fácil eliminar en 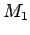 y en
y en 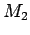 todas las dependencias de símbolos superflues antemano en caso que haya.
todas las dependencias de símbolos superflues antemano en caso que haya. 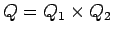 , es decir, el producto cartesiano de los estados de
, es decir, el producto cartesiano de los estados de 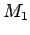 y
y 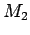 .
.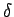 es la función de transición con
es la función de transición con
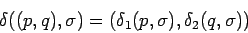
para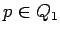 ,
, 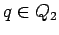 y
y 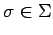 .
.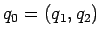 , es decir, la pareja de los dos estados iniciales
, es decir, la pareja de los dos estados iniciales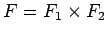 , es decir, todas las parejas donde ambos estados son estados finales de ambos autómatas.
, es decir, todas las parejas donde ambos estados son estados finales de ambos autómatas.
Comentarios
Publicar un comentario